© 2020

Welcome

Research, development, consulting and training in computational structural analysis

The reason you are here …

Whether you are searching for the simulation analyst in biomedical or a structural performance, the finite element developer, composite material designer, building energy performance analyst, you are in the right place. We are happy that you are here, helping us to grow.

Consulting

• Numerical modeling of the physical laws and implementation into efficient code • Thermo-mechanical Finite Element (FEM) development • Thermo-mechanical Finite Element (FEM) Analysis, compliance with standards • Composite material parameters identification, testing, and simulation • Topology design: shape/material, cost/performance analyses of structures • Assessment of carrying capacity and fatigue strength. • Minimization of energy consumption and CO2 emission in buildings and heating devices

Developing

• FEMIX - Reliable multifield multiscale mixed finite element method for thermo-mechanical analysis of engineering and biomedical structures and components of isotropic, anisotropic and orthotropic materials, layer-wise or particle reinforced composites, non- sensitive on finite element shape and aspect ratio, fast and accurate • One to one bridging of FEMIX with molecular dynamics for multiscale analysis of structures over the scale

Student page

Building Physics (Bach.) Energy Efficiency (Bach.) Plate and Shell Theory (Bach.) FEM Finite Element Method (MSc) Computational Mechanics (PhD) Numerical Modeling (MSc)

About me

Academic and Consultant in the cutting edge Structural Engineering Calculations, Finite element developer. CV

“The structural performance simulation is accurate to the limit of the analyst knowledge to accurately interpret it and simulate it.” Dubravka Mijuca

Dubravka Mijuca

CAE Analyst

More than 20 years of academic and industrial experience. Portfolio FEA

© 2020

Services

“ Contemporary structural engineering analysis by the use of the Computer-aided engineering (CAE) software. “

Simulate structure not the mathematical interpretations

The client always need accurate result. He is usually not aware of the nature of techniques that will be used to give them report. The particular responsibility is on the analyst.

Design the composite that meet your goals

Composites are made of matrix and reinforcement. The type of materials used and volume fraction is essential for the cost/weight/performance success. With the material parameter and performance simulation you are drastically cut the cost.

Simulate your building energy needs and CO2 emission

If you have apartment or house or greenhouse or a pool or a gym or a space ship you need to make it comfort to use. Simulate cheaply the energy needs for desired comfort prior to building.

The best structural design for the lowest investment

The trial and error process in engineering is to much expensive for the clients who are not externally financed. If so, you are on the right place.

© 2020

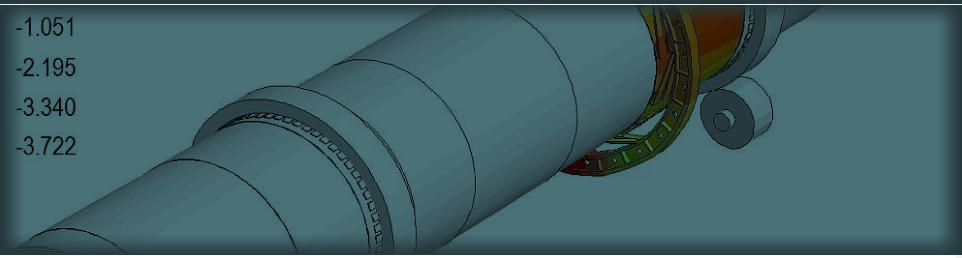
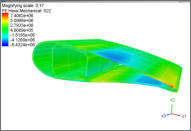
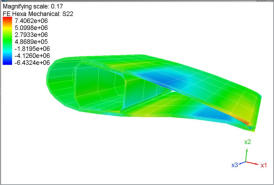
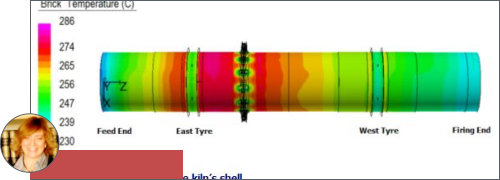
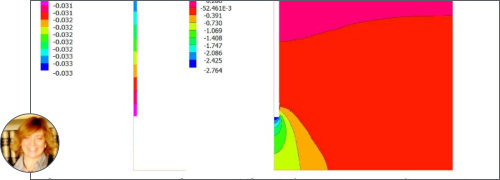
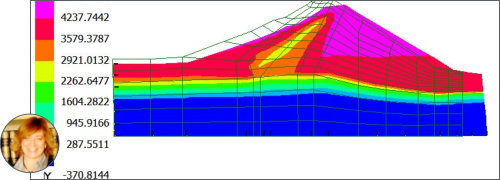
Code FEmixHC

FEmixHC is a reliable and accurate general-purpose program for thermo-elastic analysis of simple and complex structures, in medical or engineering applications. It does not require nice mesh, the mesh can be totally distorted and multiscale. It is suitable for compressible and totally incompressible materials, homogeneous, isotropic, anisotropic and orthotropic, and composites. It simulates without any simplifications, homogenizations, or trick up and tuneups, or reduced integration.

Applications in cutting edge and standard model problems:

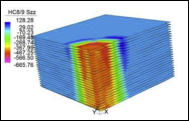
Incompressible - vascular vessels O-ring, rubber Fluid - solid interaction EM - solid interaction Melting point behavior Bi-metals -interfacial stresses Multiscale composite analysis with and/or without homogenization Impact protectors One-to-one bridging with molecular dynamic - nanoindentation

Publishing

• Mijuca D (1999) On The Main Properties Of The Primal-Mixed Finite Element Formulation, FACTA UNIVERSITATIS. 2(9) 903 - 920 UDC 518.12 532.12 539.3 • Mijuca D (2001) A New Primal-Mixed 3d Finite Element. Facta Universitatis 3(11) 167-178 • Mijuca D (2004) On Hexahedral Finite Element HC827 In Elasticity. Computational Mechanics 33(6) 466-480 • Mjuca D (2006) On Primal-Mixed formulation in Elasticity and Thermoelasticity. Monograph • Mijuca D (2010) On A New 3D Primal-Mixed Finite Element Approach For Thermal Stress Analysis Of Multi-Layered Geometrically Multiscale Structures. Finite Elements in Anal. • Mijuca D et al (1997) Some Remarks On The Energy Norm And Z-Z Error Estimator. SOLID MECHANICS. VOL LXXVII 3 254-262 YU ISBN 86-7025-263-5. • Mijuca D et al (1998) On the efficiency of the primal-mixed finite element scheme (in 2d) Conference CST'98 • 12/17/2019 10:2 • Mijuca D et al (1999) On The Main Properties Of The Primal-Mixed Finite Element Formulation. Facta Universitatis 2(9) 903 - 921 • Mijuca D et al (2005) A Novel One-To-One Multiscale Approach to Computational Mechanics of Matertals. WON Conference 180- 186.pdf • Mijuca D et al (2006) Finite Element Simulations in Elastic and Heat Transfer Analysis. NEC Report • Mijuca D et al (2007) A Novel Primal-Mixed Finite Element Approach For Heat Transfer In Soids. Computational Mechanics 39(4) 367-381 • Mijuca D etal (2011) On Accurate And Time Efficient Solution OF Primal Mixed Finite Element Equations In Multiscale Sold Mechanics. International journal for Numerical Methods in Biomedical Engineering 27(1) 95-112

Recent Citations

• Cornejo, Alejandro, Mataix Vicente, Zarate Francisco. (2019) Onaate, Eugenio. Combination of an adaptive remeshing technique with a coupled FEM-DEM approach for analysis of crack propagation problems. Computational Particle Mechanics. 10.1007/s40571-019-00306-4 • Ilya Telyatnikov (2019) Modeling of deformation processes in lithospheric structures during their static interaction. THERM SCI. • Masrat Bashir, Adnan Qayoum, Shahid Saleem (2019) Analysis of frictional heating and thermal expansion in a disc brake using COMSOL. J Phys Conf • Qiang Xi. Zhuo-Jia Fu, Timon Rabczuk (2019) An efficient boundary collocation scheme for transient thermal analysis in large- size-ratio functionally graded materials under heat source load. COMPUT MECH • Thi Huyen Cham Le, Michele D’Ottavio, Philippe Vidal, Olivier Polit (2018) Robust Displacement and Mixed CUF-Based Four- Node and Eight-Node Quadrilateral Plate Elements. In book: Analysis and Modelling of Advanced Structures and Smart Systems. DOI: 10.1007/978-981-10-6895-9_6 • A Sinu, Sundararajan Natarajan, K Shankar (2018) Quadratic serendipity finite elements over convex polyhedra. International Journal for Numerical Methods in Engineering 113(1):109–129 DOI: 10.1002/nme.5605 • James Liu, Graham Harper, Nolisa Malluwawadu, Simon John Tavener (2018) Lowest-order weak Galerkin finite element method for Stokes flow on polygonal meshes. Journal of Scientific Computing 78(3)1917–1941 • Bishnu Prasad Lamichhane,,Michael H. Meylan (2017) A new MITC finite element method for Reissner--Mindlin plate problem based on a biorthogonal system DOI: Proceedings of the 18th Biennial Computational Techniquesand Applications Conference.issn1445-8810 10.21914/anziamj.v58i0.11754 • Wojciech Gilewski, Marta Sitek (2017) Plate Finite Element with Physical Shape Functions: Correctness of the Formulation. Archives of Civil Engineering 63(3). 10.1515/ace-2017-0026 • Eric Li, Z. C. He, G. R. Liu (2107) Evaluation of the stiffness matrix in static and dynamic elasticity problems. Acta Mechanica 229(1) DOI: 10.1007/s00707-017-1977-2 • Minghao Li, Dongyang Shi, Ying Dai (2016)The Brezzi–Pitkäranta stabilization scheme for the elasticity problem. Journal of Computational and Applied Mathematics 286. DOI: 10.1016/j.cam.2015.02.024 • Kamel Meftah, , Lakhdar Sedira, Wajdi Zouari, Mabrouk HECINI, Mabrouk HECINI (2015) A multilayered 3D hexahedral finite element with rotational. European Journal of Computational Mechanic. s DOFs. DOI: 10.1080/17797179.2015.1089462 • Miguelk Cervera, Michèle Chiumenti, Ramon Codina (2010) Mixed Stabilized Finite Element Methods in Nonlinear Solid Mechanics. Part I: Formulation. Computer Methods in Applied Mechanics and Engineering 199(37):2559-2570. DOI: 10.1016/j.cma.2010.04.006

It can be integrated seamlessly

It can be integrated seamlessly before any advanced calculation tools for fracture, fatigue, wearing, aging or else. The motive could be: • mesh independent, • HEXA mesh is made from tetra without worry about the quality of the mesh, not prone to any kind of locking (shear, volumetric ...), • no need for stress recovery technique, • heat flux and stresses are primal variables as temperature and displacement and of the same accuracy, • it allows boundary conditions per stresses for the direct transfer of initial stresses from thermal, EM, or CFD calculations, • it is multiscale and allows one-to-one bridging with atomistic simulations without spuriousity or need for periodic boundary conditions. • it gives more accurate insight into interfacial stresses.

Consulting

Here is the consulting price list. The computer solution time is not charged. The analysis is performed in the software of your choice, renting software price is usually 10% of the simulation cost and is paid by the client.

FEA analysis

Transient heat transfer, mechanical, thermo-mechanical. Steady-state, static, transient heat, dynamic, linear and nonlinear per geometry and material.

Composite tailoring

Identification/optimization of the matrix and or reinforcement to meet the client's special needs.

DesignBuilder/E+ analysis

Calculation of the building's heat loss and gains and CO2 emission.

© 2020

© 2020

Education • High school - Mathematical gymnesium Belgrade (1983) • Graduated Mechanics of Deformable Bodies, Department of Applied Mechanics, Faculty of Mathematics, University of Belgrade (1989) Diploma title: On theory of plates and shells • MSc Mechanics of Deformable Bodies, Department of Applied Mechanics, Faculty of Mathematics, University of Belgrade (1995), Final work title: Continual interpretation of the solid body stress state calculated by the finite element method. • PhD Computational Mechanics, Department of Applied Mechanics, Faculty of Mathematics, University of Belgrade (1999), Thesis title: Primal-Mixed finite element scheme in mechanics of solid bodies

Courses • Statics, Strength of Materials 1990 - 1996 • Tensor Calculus, Continuum Mechanics 1997 - 1998 • Theory of Elasticity 1998 - 1999 • Mechanics of Materials 2000 - • Statistics and Probabilistic, 2003 - 2005 • Mathematics I 2005 - 2007 • Didactics in Mathematics 2005 - 2007 • Computational Mechanics 2000 - 2007 • Mechanics 1 - 2007-... • Building Physics 2007 -... • Energy Efficiency in Buildings 2008 - ... • Theory of plates and Shells 2009-... • Finite element Method 2010- • Numerical modeling 2010- • Higher Course Computational Mechanics 2000 - • Methods in Scientifics Research 2009- • Sustainable Development 2010- • Special Course in Energy Efficiency in Buildings 2010- Functions • General Secretary of Yugoslav Society of Mechanics 2003 - 2006 • Member of Presidency of the Serbian Society of Mechanics 2006 - 2009 • Vice President of Serbian Society of Computational Mechanics 2006 - • Dean of the Faculty of Civil Construction Management, University UNION, Belgrade, 2007-2008 Honors and Awards • The honors of Yugoslav Society of Mechanics for 15 years of engagements in running the Seminar of Rheology, as a secretary from 1991- 2000 and leader 2002-2005 (November 14, 2005)

Professional Society Membership

• SSM Serbian Society of Mechanics • AFEMS International Association for Engineering Analysis Community • DIVK Serbian Society in Structural Integrity and Life

Coordinator of

• Membership of University of Belgrade NAFEMS, 2001-2007

Leader of

• Seminar for Rheology Department of Mechanics Faculty of Mathematics University of Belgrade, 2000-2007

Other Activities

• Finite Element Training Courses Instructor (VND inženjering i konsalting) • Distributor of LUSAS Finite element software package • Distributor of Straus7 (Strand7) Finite element software package • Distributor of DesignBuilder for Simulation software for Integral Efficiency of Buildings • Distributor of CMS IntelliCAD • Advisor for Student Entrepreneurships Activities, Faculty of Mathematics, University of Belgrade 2002-2004

Research Interest

• Computational methods in applied sciences and engineering • Finite elements methods in multifield computational mechanics • Global stress recovery techniques • Primal-mixed finite element approach in thermo-mechanical analysis • Multiscale analysis in engineering and bioengineering • Numerical simulation of the energetic efficiency of buildings

Projects in Fields of Basic Research

• Contemporary Problems in Mechanics, No.0402, 1992 - 1995 • Contemporary Problems in Mechanics, No.04M01, 1995 - 1999 • Development and implementation of the new reliable methods in mechanics of solid and fluids, No.1865, (principal investigator) 2002 - 2006. • Mathematical methods and algorithms for 3d contours recognitions, No. 1645, 2002 - 2006 • Mathematical Models and Optimization Methods with Applications, Project No. 144007, 2005 -

Projects in Energetic Efficiency

• Mathematical modelling and development of methods and techniques for diagnosis of energetic efficiency in existing and new buildings. No. NPEE813-197b, 2003-2006 (principal investigator) • Implementation of the European regulative in heating and cooling of buildings No. NPEE 283011, 2006- (principal investigator)

International Projects

• FP5 framework EC: FENet - A thematic network for promoting best practice industrial application of finite element technology, Project number: GTC2 2000 33057, 2001-2005 (local principal investigator) • Deutsche Forschungsgemeinschaft Geforderte, DFG-Projekt Schm 746/74-1, Improved toughness balance of nano particle filled polyamid composite simulation supported properties/morphology correlation 2012- • SPP 1420 Numerical Simulation of Open Cell Foams in passive impact protection 2012-2013

Projects in Fields of Innovative Research

• Software for Continual Stress State Representation, No.I.1, 1556. 1997

Industrial projects

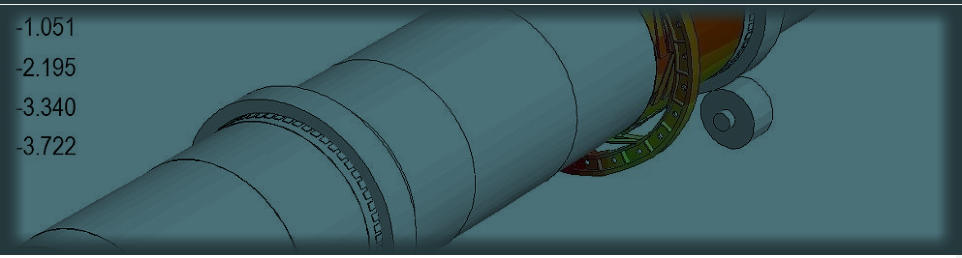
• Integral Energy Efficiency Assessment of the Building Site Block 34 in New Belgrade, Principal Integral Energy Efficiency analyst, Numerical simulation of energy performance in buildings with DesignBuilder Software, Ministry of Science Republic of Serbia, 2004 • Integral Energy Efficiency Assessment of the Building Site Block 29 in New Belgrade, Principal Integral Energy Efficiency analyst, Numerical simulation of energy performance in buildings with DesignBuilder Software, Ministry of Science, Republic of Serbia, 2006 • Integral energy efficiency report for the residential house in Ljube Jovanovića 7, Senjak, Belgrade, Principal Integral Energy Efficiency analyst and Consultant, Integral simulation of building energy performance and consulting in selection of materials for building envelope for best cost/energy performance ratio, Private Investor, Senjak, Belgrade, 2010 • Integral Energy Efficiency Assessment of the old building built in 1933 in central zone of Belgrade, Principal Integral Energy Efficiency analyst, Numerical simulation of energy performance in buildings with DesignBuilder Software, Ministry of Science, Republic of Serbia, 2006 • Geotechnical Investigation and Design of Reconstruction of Earth Dam Banjani (H= 30m L=65m), Principal Finite Element analyst, Consulting in displacement and stress state of the dam, Ministry of Agriculture, Forest and Water, Local Municipality of Gornji Milanovac, Serbia, and VND engineering and consulting, 2003 • Lime kiln upgrade - Recuperation, Principal Finite Element analyst, Consulting in optimum design of heat recuperation system, IT -1 PTY LTD Australia, for One Steel Comp. Australia, 2003 • Migration of software ASCOS - building fire protection and smoke control system to windows operating platform and implementation of new modules, Principal programmer and finite element developer, Programming and Testing of fire protection engineering tools for hazard Estimation, CIP Institute Belgrade, Serbia, 2006 • Integrated assessment of detailed Pellet Rotary Kiln behavior including Girth Gear (GG) Flange and Position Bolts, Principal Finite Element analyst And Consulting, Consulting in detailed kiln behavior toward optimum design of flange and position bolts , IT -1 PTY LTD Australia, for One Steel Comp. Australia, 2007 • Engineering simulation of stresses and displacement of embedded fiber optic sensor in composite material under impact, Principal Finite Element analyst, Fully 3D Finite Element analysis of indentation of aramid composite material with embedded optic fibers, ETF, Belgrade, Serbia, 2007 • Integrated assessment of detailed piles behavior, soil-pile interaction, Principal Finite Element analyst, Consulting in behavior of soil-pile interaction for the proposed and optimal design of pile structure toward minimization of steel mass, Fablive, Budva, Montenegro, 2008 • Finite element Structural analysis of the wagon of the Falns type, Principal Finite Element analyst, Full static and dynamic finite element stress analysis and verification under EN/ISO/IEC 17025 norm , Institut Kirilo Savic, Belgrade, Serbia, 2009 • Code for environment for AUTOMATIC multidisciplinary thermo-elastic optimization of electronic components , Principal programmer , Programming and Testing, CADLM, 2009 • Axel boxes railway vehicle verification, BA172, for Kovis, Slovenia, Principal Finite Element analyst, Full static and dynamic finite element stress analysis and verification under EN/ISO/IEC 17025 norm , KOVIS, Slovenia, 2010 • Fire protection/structural analysis of doors , Principal Finite Element analyst, Full transient heat transfer and thermoelastic analysis, Samika, Valjevo Serbia, 2010 • Axel boxes railway vehicle verification, Y25-25T, for Kovis, Slovenia, Principal Finite Element analyst, Full static and dynamic finite element stress analysis and verification under EN/ISO/IEC 17025 norm, KOVIS, Slovenia, 2011 • Design of a new foam like impact protection system , Principal designer and finite element analyst, The CAD designing and FE analysis of the foam like structure with optimal retaining of structural integrity under impact, IMWF, Stuttgart, Germany, 2012 • Integrated assessment of detailed piles behavior, soil-pile interaction Block 67a, phase I, Principal Finite Element analyst, Consulting in behavior of soil-pile interaction for the proposed and optimal design of pile structure toward minimization of steel mass, EX ING B&P, Belgrade, Serbia, 2014 • Integrated assessment of detailed piles behavior, soil-pile interaction Block 67a, phase II, Principal Finite Element analyst, Consulting in behavior of soil-pile interaction for the proposed and optimal design of pile structure toward minimization of steel mass, EX ING B&P, Belgrade, Serbia, 2015 • Integrated assessment of detailed piles behavior, soil-pile interaction Block 67a, phase III, Principal Finite Element analyst, Consulting in behavior of soil-pile interaction for the proposed and optimal design of pile structure toward minimization of steel mass, EX ING B&P, Belgrade, Serbia, 2016 • Integrated assessment of detailed piles behavior, soil-pile interaction Block 43 - SIRIUS, Principal Finite Element analyst, Consulting in behavior of soil-pile interaction for the proposed and optimal design of pile structure toward minimization of steel mass, STRABAG, 2016 • Integrated assessment of detailed piles behavior, soil-pile interaction for IKEA , Principal Finite Element analyst, Consulting in behavior of soil-pile interaction for the proposed and optimal design of pile structure toward minimization of steel mass, STRABAG, 2016 • Integrated assessment of detailed piles behavior, soil-pile interaction for EXING , Principal Finite Element analyst, Consulting in behavior of soil-pile interaction for the proposed and optimal design of pile structure toward minimization of steel mass, location Vozdovac "Vozdove kapije", Belgrade, 2017

Reviewer of

• Zentralblatt MATH • Facta Universitatis, Series Mechanics, Automatic control and Robotics • Matematički Vesnik Beograd • Journal `Thermal Science` Vinča, Serbia • Journal `Energy and Buildings` Elsevier • Mathematical Problems in Engineering • Journal of Mechanics of Materials and Structures • Finite element and design, Elsevier

Editorial Jobs

• Dubravka Mijuca, Stevan Maksimovic. Book of Abstracts in Paper Form: The First International Conference on Computational Mechanics In memory of Prof. dr Mladen Berkovic, ISBN 86-7589-043-5, • Dubravka Mijuca, Stevan Maksimovic. Book of Papers In Electronic Form: The First International Conference on Computational Mechanics In memory of Prof. dr Mladen Berkovic, ISBN 86-7589-042-7,

Organized workshops

• New Trends in Multidisciplinary Design Optimization May, 19-21 2003, Faculty of Mathematics, University of Belgrade • Review in Inelastic Analysis of Structures October, 13-15 2003, Faculty of Mathematics, University of Belgrade • In conjunction with LUSAS (www.lusas.com), a presentation of its LUSAS Bridge and LUSAS Civil & Structural softwaretook place at the Engineering Chamber, Kneza Milosa 9/II, 11000, Belgrade on 4th September 2007. Presentations was given on the key features and facilities in LUSAS software that can be of use to you in your design office or university. Attendance at this event was free.

Organized conferences

• First International Conference on Computational Mechanics (CM’04) Belgrade, Serbia, November, 15‑17, 2004, In memory of Prof.dr Mladen Berković. President of the organizing committee • Organizer of the Special Session Finite element simulation of the high risk constructions, experiences and problems, within the 2nd WSEAS International Conference. on APPLIED and THEORETICAL MECHANICS (MECHANICS '06), Venice, Italy, November 20-22, 2006. www.worldses.org/conferences/2006/venice/mechanics. President of the organizing committee • SYMPOSIUM: CONTEMPORARY MATHEMATICS, Faculty of Mathematics, University of Belgrade, December 18-20 (2008). Member of the organizing committee

Journal Publications and Theses

• Mijuca D, Berković M (1994) Coordinate independent stress recovery procedure. The PAMM's periodical BAM 1026/94, ISSN 0133-3526 • Mijuca D (1995) Continual coordinate independent finite element interpretation of stress state in solid body. MS.C. Thesis, University of Belgrade , (in Serbian) • Mijuca D et al (1997) Some Remarks On The Energy Norm And Z–Z Error Estimator. SOLID MECHANICS. Vol. LXXXVII 3 254- 262 YU ISBN 86-7025-263-5 • Mijuca D, Berković M (1997) Stress recovery procedure based on the known displacement. Facta Universitatis, Series Mechanics, Automatic control and Robotics, 7(2):513-523, ISSN 0354-2009 • Mijuca D, Berković M and Drašković Z (1998) A direct sparse solution of the mixed finite element equations. Computer Assisted Mechanics and Engineering Science, 5:21-30, ISSN1232-308X • Mijuca D (1998) Advances in computational structural mechanics. Facta Universitatis, Series Mechanics, Automatic Control And Robotics, 2(8): 811-816 ISSN 0354-2009 • Mijuca D (1999) Primal-mixed finite element approach in solid mechanics. Ph.D. Thesis, Faculty of Mathematics, Belgrade (in Serbian) . • Mijuca D, Berković M (1999) On the main properties of the primal-mixed finite element formulation. Facta Universitatis Series Mechanics, Automatic Control And Robotics, (2)9: 903-920, ISSN 0354-2009. • Mijuca D (1999) MEMORY ON PROFESSOR DR MLADEN BERKOVIĆ, Facta Universitatis Series Mechanics, Automatic Control And Robotics, 2(9) 1015-1017 • Mijuca D, Berković M and Grozdanović I (2001) Some continuous stress mixed formulations and inf-sup test. Computer Assisted Mechanics and Engineering Science, Vol.8, 141-153 , ISSN1232-308X. • Mijuca D (2001) A new primal-mixed 3d finite element. Facta Universitatis Series Mechanics, Automatic Control And Robotics, 3(11):167-178, ISSN 0354-2009. • Mijuca D (2002) On the reliability of the new finite element HC8/27. Facta Universitatis Series Mechanics, Automatic Control And Robotics, 3(12): 385-396 , ISSN 0354-2009 • Rakin M, Baras J, Vukasinovic M, Mijuca D (2003) Optimization of lactic-acid fermentation of beetroot juice and brewer’s yeast autolysate. Roumanian Biotechnological Letters. 8(5-6): 1421-1430 • Mijuca D., Gajić D, Vukobrat M (2003) Trodimenziona metoda konačnih elemenata u termičkoj analizi građevinskih objekata. Termotehnika, 29(1-4):119-134 • Mijuca D (2004) On hexahedral finite element HC8/27 in elasticity. Computational Mechanics, 33(6): 466-480, ISSN: 0178- 7675 • Mijuca D, Ziberna A and Medjo B (2005) A new multifield finite element method in steady state heat analysis. Thermal Science, Vol. 9(1): 111-130 • Mijuca D (2006) On Dimensional Reduction in Multiscale, Finite Element and Atomistic, Analysis in Solid Mechanics. WSEAS TRANSACTIONS on APPLIED and THEORETICAL MECHANICS, 1(1):.16-25, . ISSN 1991-8747 • Mijuca D, Ziberna A and Medjo B (2007) A Novel Primal-Mixed Finite Element Approach for Heat Transfer in Solids, Computational Mechanics, 39(4):367-381. DOI 10.1007/s00466-006-0034-0 • Mijuca D (2008) On a Reliable Finite Element Approach in Multiscale Multimaterial Solid Thermo- Mechanics, Journal of the Serbian Society for Computational Mechanics. 2(1):44-62 • Mijuca D (2009) A novel finite element scheme in the analysis of thermal barrier coating components. Problems of Nonlinear Analysis in Engineering Systems - 1(31) • Mijuca D (2010) On a new 3D primal-mixed finite element approach for thermal stress analysis of multi-layered geometrically multiscale structures. Finite Elements in Analysis and Design 46: 299-310, DOI: 10.1016/j.finel.2009.11.001. • Duff IS and Mijuca D (2011) On accurate and time efficient solution of primal-mixed finite-element equations in multiscale solid mechanics. International journal for Numerical Methods in Biomedical Engineering, 27(1):95-112, DOI: 10.1002/cnm.1296

SciTopics page Elsevier

• Mijuca D (2010) Mutifield and multiscale simulations of engineering and biological sytructures toward virtual reality , Retrieved April 20, 2010

Books

• Mijuca D, Berković M and Drašković Z. Displacement based continuous stress recovery procedure. Advances in Finite Element Technology, Ed. B.H.V.Topping, Civil-Comp Press, 127-134 (1996) ISBN 0-948749-41-5 • Mijuca D, Berković M. Some remarks on the energy norm and Z-Z error estimator. SOLID MECHANICS, , Vol. LXXXVII, book 3, 254-262 (1997). YU ISBN 86-7025-263-5 • Mijuca D, Berković M. On the efficiency of the primal-mixed finite element scheme. Advances in Computational Structured Mechanics, Ed. B.H.V. Topping, Civil-Comp Press, pp.61-69, (1998). ISBN 0-948749-57-1, • Velimir Simonovic, Dubravka Mijuca, Metodika nastave matematike, (2011), Zavod za udzbenike Beograd, Cobiss 184385548, ISBN 978-86-17-17503-8 • Mijuca D. On Primal-Mixed formulation in Elasticity and Thermoelasticity, published by Faculty of Mathematics University of Belgrade (2006)

Invited / Plenary Lectures

• Mijuca D, Berković M (1996) On the Numerical Integration of Z-Z type Error Indicators , Second Serbian-Greek Symposium on Solid Mechanics, Belgrade . • Mijuca D, Berković M (1997). Efficient and reliable mixed finite element analyses of solid continua, Euromech Colloqium 371, Bad Herrenhalb, Germany • Mijuca D, Berković M (1998) On the current state on the computational mechanics, Symposium Contemporary Mathematics, Devoted to 125 anniversary of Faculty of Mathematics and to 190 years of teaching of mathematics in Serbia • Mijuca D (2002) A Novel Stress Results In The Finite Element Analysis Of Clamped Plates Obtained by Full 3D, EnginSoft, conference and user’s meeting: VIRTUAL PROTOTYPING TODAY: INDUSTRIAL IMPACT AND FUTURE TRENDS, October 12-15, Stezzano . ISBN 88-87786-01-1 • Mijuca D (2006) On dimensional reduction in multiscale, finite element and atomistic, analysis in solid mechanics, , 2nd WSEAS International Conference. on APPLIED and THEORETICAL MECHANICS (MECHANICS '06), Venice, Italy, November 20- 22 www.worldses.org/conferences/2006/venice/mechanics • Mijuca D (2006) ON THE ISSUE OF MULTISCALE ROBUSTNESS IN COMPUTATIONAL MECHANICS. Seminar in honor of 60 years of founding the Mathematical Institute of Serbia, December 13- 15 • Mijuca D (2007) On the Issue of Multiscale Robustness in Computational Mechanics, by Dubravka Mijuca. Minisymposia: Computational Methods in Structural Analysis and Optimization by FEM, 1st INTERNATIONAL CONGRESS OF SERBIAN SOCIETY OF MECHANICS 1st ICSSM-2007, April, 10-13 Proceedings of the 1st International Congress of Serbian Society of Mechanics, ISBN 978-86-909973-0-5, pp. 675-682. (Presentation PPS) • Mijuca D (2008) (2008) On the multiscale simulations by mixed finite element method in thermoelasticity. 6th International Conference CoNuSS-2008 of Nuclear Society of Serbia , Session Nuclear Fusion, September 22-25, Belgrade, Serbia; http://nss.vin.bg.ac.yu/CoNuSS2008.htm • Mijuca D (2009) On Reliable Continuum Mechanics Formulations in Multiscale Simulations of Solids. Plenary lecture at the 4th IASME / WSEAS International Conference on CONTINUUM MECHANICS (CM'09), Cambridge, UK, February 24-26

Invited Lectures at Workshops

• Mijuca D (2002) Lecture at First SimLab Course on Parallel Numerical Simulation, CSM: The Basic Equations and Applications, Faculty of Mechanical Engineering, University of Belgrade, February 28 • Mijuca D (2006) Lecture at Fifth SimLab Course on Parallel Numerical Simulation About Reliability of Numerical Simulation Approaches in the Multiscale Analysis of Complex Engineering Structures, Faculty of Mechanical Engineering, University of Belgrade, October, 1-7

Invited Lectures at International Seminars

Mijuca D. About Reliability of Primal and Mixed Finite Element Schemes in the Thermo-mechanical Analysis of Solid Bodies, Department of Mechanical and Materials Engineering, Mechanical and Materials Engineering Graduate Student and invited Speaker Seminar Series, Florida International University 20 June, 2005 Mijuca D. On the Use of Fully Three Dimensional Multifield Mixed Finite Element Scheme in Multiscale Structural and Building Energy Efficiency Simulations. NIST - National Institute of Standards and Technology, USA MCSD Seminar Series Thursday, June 28, 2007 15:00-16:00, Building 101, Lecture Room A. Gaithersburg. Thursday, 13:00-14:00, Room 4550. Boulder, June 28, 2007 Mijuca D. On the multiscale simulations by mixed finite element method in thermoelasticity. CERFACS - European Centre for Advanced Research and Advanced Training in Scientific Computation, April 21, 2008 Mijuca D. On a reliability of the finite element simulation from the megastructure continuum to nanoscale levels. ARISTOTLE UNIVERSITY OF THESSALONIKI. 29 April 2009. Mijuca D. On a new multiscale finite element approach in a simulation of multimaterials under thermomechanical loading. University of Stuttgart, IMWF, 8 December 2011

Fully-Refereed International Conference Proceedings

Mijuca D, Berkovic M and Draškovic Z (1996) Displacement based continuous stress recovery procedure , CST96 The Third International Conference on Computational Structure Technology, Budapest, 21-23 August; also published in Advances in Finite Element Technology, ISBN 0-948749-41-5, Ed. B.H.V.Topping, Civil-Comp Press, 127-134 Mijuca D, Berković M and Drašković Z (1996) A direct block sparse solution of the mixed finite element equations. Conference on Numerical Methods and Computational Mechanics in Science and Engineering, Miskolc, Hungary Mijuca D, Berković M; (1998) An efficient continuous stress mixed model based on the Reissner’s principle. Computational Mechanics, New Trends and Applications, pp.1-12, WCCM Argentina Mijuca D, Berković M (1998) A posteriori error estimates of the recovered finite element solution. Conference on Numerical Methods and Computational Mechanics, pp.7-9, Miskolc, Hungary Mijuca D, Berković M (1998) On the direct solution of the Primal-mixed finite element equations. Conference on Numerical Methods and Computational Mechanics, pp.67-69, Miskolc, Hungary Mijuca D (2001) A new primal-mixed 3d finite elements, NAFEMS World Congress 2001, 24 - 28 April 2001 - Lake Como, Italy, pp 1041-1051. Mijuca D (2002) A New Reliable 3D Finite Element in Elasticity. Proceedings of the Fifth World Congress on Computational Mechanics (WCCM V), July 7-12, Vienna, Austria, Editors: Mang, H.A.; Rammerstorfer, F.G.; Eberhardsteiner, J., Publisher: Vienna University of Technology, Austria, ISBN 3-9501554-0-6, http://wccm.tuwien.ac.at/ Mijuca D, Ziberna A and Medjo B (2004) A new mixed hexahedral finite element in heat transfer analysis . First International conference in Advanced Concepts in Mechanical Engineering; 8th-10th July 2004; Iasi; Romania; BULETINUL INSTITULUI POLITEHNIC DIN IASI; Vol. L (LIV); No 6B; 167 - 173; Editors: Nicolae Badae, Ioan Giurma, Mihail Voicu, Dorel Leon Mijuca D, Gajic D and Vukobrat M (2004) On the Three-dimensional Finite Element Method in the Energy Efficiency of Building’s Envelope, 35th International Congress on HVAC, Belgrade PPS Mijuca D (2005) On The New Semicoupled Linear Static And Steady State Heat Mixed Finite Element Approaches. NAFEMS World conference, May 17-21, Malta Mijuca D, Mastilović S (2005) A Multiscale Approach to Computational Mechanics of Materials, 15th International workshop on computational Mechanics of Materials, IWCCM 15, Max-Planck-Institut für Eisenforschung GmbH, Düsseldorf, Germany, September 19 and 20, www.iwcmm15.mpie.de/program.html Mijuca D (2005) A Novel One-To-One Multiscale Approach to Computational Mechanics of Materials, Mijuca D, Sreten Mastilović, 1st International Workshop on Nanoscience & Nanotechnology IWON 2005 and 4th COSENT Annual Meeting Belgrade, November 15 - 18, pp.180-186 Mijuca D (2008) On the multiscale simulations by mixed finite element method in thermoelasticity, 6th International Conference CoNuSS-2008 of Nuclear Society of Serbia, Session Nuclear Fusion, September 22-25, Mijuca D, Kordic Dikovic N (2014) On new 3D FE methodology and verification in EOD Test. International CAE Conference, Pacengo del Garda (Verona) - Italy, 27-28 October Mijuca D. (2015) On a new unconditionally stable and fast finite element approach in thermoelasticity ready for one-to-one bridging with atomistic scale simulation procedures. International CAE Conference, Pacengo Lazise (Verona) - Italy, 19-20 October

International Conference Abstract Proceedings

Mijuca D (2003) A new primal-mixed finite element scheme in 3D thermoelasticity. The Mathematics Of Finite Elements And Applications 2003 (MAFELAP 2003). Brunel University, London , 21 - 24 June Mijuca D (2006) On the more Reliable Introduction of the Residual Stresses in the Thermo-mechanical Analysis of Layered Structures. International NAFEMS seminar Prediction and Modelling of Failure Using FEA. Risoe, Roskilde, Denmark, May 30-31. Mijuca D (2008) On the multiscale simulations by mixed finite element method in thermoelasticity. World Conference in Computational Mechanics, WCCM 08, at MInisymposium SCALE BRIDGING IN SCIENCE AND ENGINEERING, Venice, Italy, 2-7 July Mijuca D (2010) On more reliable finite element thermo-mechanical simulation of multi-layered geometrically multiscale structures. IV European Conference on Computational Mechanics - ECCM 2010 , Paris, May 16th-21th Mijuca D (2016) Interfacial Stress and its analysis by finite element method. Mini-symposium “Fracture Mechanics and Numerical Methods” Mathematical Institute of SASA and Project OI 174001, Belgrade, Serbia, November 16, 2016 Fully-Refereed National Conference Proceedings ▲ Mijuca D (1995) Graphical postprocessor in FEM with new stress smoothing modules, Mijuca D, Berković Mem, YU INFO'95, pp. 333-338, Brezovica, (in Serbian) Mijuca D Berković M (1995) Some stress recovery procedures in the classical FE analysis. XXI Yugoslav Congress on Theoretical and Applied Mechanics, C5-87, pp 512-517, Niš Mijuca D, Berković M (1997). On the efficiency of the stress projection procedure. XXII Yugoslav Congress on Theoretical and Applied Mechanics, pp.41-47, Vrnjačka Banja Mijuca D (2001) A new stable Taylor-Hood finite element in linear el XXIII Yugoslav Congress on Theoretical and Applied Mechanics, Belgrade Mijuca D, Gajić, D, Kordić-Diković N, Jojić I and Djurović-Petrović M (2005) Prikaz metodologije i rezultata simulacije potrošnje energije i rada sistema za grejanje i klimatizaciju na oglednom stambenom objektu u Novom Beogradu, 35th International Congress on HVAC, Belgrade, pp.107-115. Mijuca D (2007) On the Issue of Multiscale Robustness in Computational Mechanics, by Dubravka Mijuca. Minisymposia: Computational Methods in Structural Analysis and Optimization by FEM, 1st INTERNATIONAL CONGRESS OF SERBIAN SOCIETY OF MECHANICS 1st ICSSM-2007, April, 10-13 Proceedings of the 1st International Congress of Serbian Society of Mechanics, ISBN 978-86-909973-0-5, pp. D. Mijuca (2009) On the reliable and efficient thermal stress finite element procedure in multiscale analysis of solids. 2nd International Congress of Serbian Society of Mechanics (IConSSM 2009) Palic (Subotica), Serbia, 1-5 June 2009.

National Conference Abstract Proceedings

Mijuca D and Berkovic M (1998) Efficiency of the coordinate independent FE primal-mixed scheme. XIII Conference on Applied Mathematics, 82-82, Igalo Mijuca D (2000) A new pimal-mixed 3d finite element in analysis of plates and shells. 10th Congress of Yugoslav Mathematician, pp 102, Belgrade. Mijuca D (2002) On the Stability of the primal-mixed 3d finite element scheme. XV Conference on Applied Mathematics, 17-172, Zlatibor Mijuca D (2002) On the stability of the primal-mixed finite element scheme. XV Conference on Applied Mathematics, Zlatibor, 17-17 Mijuca D and Ziberna A (2004) On The New Solution Approach In The Steady State Heat Problem. XI Kongres matematicara Srbije i Crne Gore, Petrovac, 28.Sept.-3.Oct Mijuca D (2004) Analiza temperatura i naprezanja u omotacu rotacione peci. Godisnja Konferencija Drustva Za Integritet I Vek Konstrukcija (DIVK) 13-15 Oktobar

Lectures on Domestic Seminars

About Bone remodelling. Seminar for Rheology, Faculty of Mathematics, University of Belgrade, April 27, 1990. About Finite Element Method in ALGOR, with Berkovic M., Seminar for Rheology, Faculty of Mathematics, University of Belgrade, October 11, 1994. About stress recovery after classical finite element approach, with Berkovic M, Seminar for Rheology, Faculty of Mathematics, University of Belgrade, November 22, 1994. About inconsistency in calculation of membrane stresses and deformations in shell finite elements based on primal finite element approach. With Berkovic M, Seminar for Rheology, Faculty of Mathematics, University of Belgrade, March 21, 1995. New findings in stress recovery after classical finite element approach, With Berkovic M, About stress recovery after classical finite element approach, October 31, 1995. On the Numerical Integration of Z-Z type Error Indicators , Mijuca D, M. Berkovic. Seminar for Rheology, Faculty of Mathematics, University of Belgrade , June 18,1996. Impressions from The international Conference on computational structures Technology CST’96 Budapest, Seminar for Rheology, Faculty of Mathematics, University of Belgrade, September 24,1996. Some remarks on energy norm and a posteriori error estimation. With Berkovic M. Seminar for Rheology, Faculty of Mathematics, Belgrade , May 6,1997. About numerical results obtained by solving the two-field method equation system. With Berkovic M, Seminar for Rheology, Faculty of Mathematics, University of Belgrade , September 23,1997. About some anomaly of stress numerical solution in the case of primal-mixed finite element method , Mijuca D, M. Berkovicem, Seminar for Rheology, Faculty of Mathematics, University of Belgrade , February 17, 1998. Software for global coordinate independent continual interpretation of stresses after displacement method in finite element analysis , With Berkovic M, Seminar for Rheology, Faculty of Mathematics, University of Belgrade , April 21,1998 Primal-mixed finite element in solid mechanics Seminar for applied mathematics, Mathematical institute SANU, Department of Mechanics. November 18, 1998. A new pimal-mixed 3d finite element, Seminar for Rheology, Faculty of Mathematics, Belgrade , 10.10.2000 d finite element, Seminar for Rheology, Faculty of Mathematics, University of Belgrade , October 10, 2000. A reliable numerical designing - the shortest way from concept to reality , Seminar for RheologyLow tests. The new reliable finite element schemes. Seminar for Rheology, Faculty of Mathematics, University of Belgrade, November 15, 2001. High test of the new reliable 3d finite element in linear elasticity . Seminar for mechanics, Mathematical institute SANU, Department of Mechanics, University of Belgrade. November 21, 2001. About contemporary finite element software packages . The society of civil engineers and technicians , Novi Sad , 18.12.2001. On the stability of finite elements HC8/27 in analysis of plate and shells , Seminar for Rheology, Faculty of Mathematics, University of Belgrade , May 28, 2002. About of the Fifth World Conference of Computational Mechanics , July 7-12, 2002 Vienna . Seminar for mechanics, Mathematical institute SANU, Department of Mechanics. December 20, 2002. On 2d and 3d finite element displacement and mixed methods in fracture mechanics . Seminar for Rheology, Faculty of Mathematics, University of Belgrade. April 15, 2003. A new approach in the solution of the thermoelasticity problems by the use of primal-mixed finite elements , Faculty of technical Sciences, Department of Mechanics, University of Novi Sad, April 18, 2003 A primal-mixed finite element method in the calculation of thermal stresses. Seminar for Rheology, Faculty of Mathematics, University of Belgrade, Jun 10, 2003. CSM: The Basic Equations and Applications, First Short Course on Parallel Numerical Simulation, Simulation Lab in Belgrade, Faculty of Mechanical Engineering, University of Belgrade. In organization of the University of Stuttgart: http://www.informatik.uni-stuttgart.de/ipvr/sgs/projekte/_simlab/simlabcourse.html Septemeber 9, 2003. A numerical simulation of the behavior of the dam "Banjani", with Nina-Kordic Dikovic . Seminar for Rheology, Faculty of Mathematics, University of Belgrade, October 28, 2003. The Primal-Mixed Finite Element Scheme In The Bimaterial Thermoelasticity, Seminar of Mechanics ,Mathematical Institute, Serbian Academy of Science; March 17, 2004. A New Mixed Finite Element Approach in Steady state Heat Analysis, with Medjo B and Ziberna A, Seminar for Rheology, Faculty of Mathematics, University of Belgrade, May 2004. On The Use Of Ma47 Solution Procedure In The Finite Element Steady State Heat Transfer Analysis, With Ziberna A, Seminar for Rheology, Faculty of Mathematics, University of Belgrade, October 2004. A novel reliable 3D primal mixed finite element scheme in the analysis of thermal barrier coating components. Mathematical Institute, Seminar of Mechanics, Mathematical Institute, Serbian Academy of Science. December 21, 2005. On more reliable finite element thermo-mechanical simulation of solid bodies over the scales. ermo-mechanical simulation of solid bodies over the scales. Seminar of Mechanics, Mathematical Institute, Serbian Academy of Science; December 16, 2009. Numerical Simulation of Open Cell Foams, Seminar of Mechanics, Mathematical Institute, Serbian Academy of Science;December 17, 2014

Technical Innovations

The contest for the best technological innovation Ministry of Science Republic of Serbia (2010), sixth place: Mijuca D et. al. Support structure - SUPORT The innovative technical solution for protection of deep excavation for foundation pits, depth up to 8m in flooded area. The contest for The best technological innovation Ministry of Science Republic of Serbia (2015), third place, Mijuca D et. al. :ACCBOX - New wireless acceleration measurement device and data acquisition for pile boring and earthquake detection.

Studies

Mijuca D, Kordić-Diković N, Jojić I, Gajić I (2005) Implementation study of the rehabilitation procedure and conservation of building’s envelope by silicon paints. Ministry of Science Serbia Mijuca D, Kordić-Diković N, Jojić I, Gajić D (2005) Evaluation study of the rehabilitation of building’s envelope by silicon paints from the aspects of the increase of energy efficiency. Ministry of Science Serbia Kordić-Diković N, Jojić I, Gajić D (2005) Evaluation study of the energy efficiency of apartment without changes. Ministry of Science Serbia Gajić D, Mijuca D, Jojić I(2005) Evaluation study of the procedure of increase of energy efficiency of experimental apartment by the replacement of windows.. Ministry of Science Serbia Mijuca D, Kordić-Diković N, Jojić I, Gajić D(2005) Numerical simulation in estimation of the energy efficiency of buildings on the experimental building site in New Belgrade (Nb.of pages. 98). Ministry of Science Serbia

Reports

Mijuca D. Medjo B, Ziberna A (2005) Finite Element Simulations in Elastic and Heat Transfer Analysis, Reports on the use of NEC SX6i Supercomputer, 27 May Mijuca D (2004) Procedural Benchmarks for Common Fabrication Details in Plate Shell Structures, contribution with HC8/9 FE results. Project EU FP5 FENET D5603 Mijuca D (2005) Report/Review on Fracture mechanics simulation software developed by Prof, Kojic group at University of Kragujevac . For National Electric Distribution Company No.2640 Mijuca D (2005) Mathematical modeling and development of methods and technique for diagnosis of energetic efficiency of existing and new buildings Project: NPEE 451-03-1549/2003-01/EE813-197B Mijuca D (2007) Report/Review on Mahematical models and software tools for fluid-dynamics and heat processes in thermo energetic equipment (Matematički modeli i softverski alati strujnodinamičkih i toplotnih procesa u opremi termoenergetskih blokova za primenu u dijagnostici stanja i predviđanju ponašanja) for need of the national electric distribution company No.II- 326/3 (2007) Duff IS and Mijuca D (2008) On the efficient solution of mixed finite element equations in geometrically multiscale thermal stress analysis. Rutherford Appleton Laboratory (RAL) RAL-TR-2008-009

Cited in

Cuomo M, Contrafatto L (2000) Stress rate for elastoplastic models with internal variables based on augmented Lagrangian regularization. International Journal of Solids and Structures 37 3935-3964 Jaroslav Mackerle, (2000) Finite element linear and nonlinear, static and dynamic analysis of structural elements - an addendum - A bibliography (1996-1999) Engineering Computations, Volume 17 Issue 3, pp. 274-351 Jaroslav Mackerle,(2001) Error estimates and adaptive finite element methods: A bibliography (1990-2000) Engineering Computations, Volume 18 Issue 5/6 pp. 802-914 V. A. Maksimyuk and I. S. Chernyshenko (2004) Mixed functionals in the theory of nonlinearly elastic shells. Volume 40, Number 11 / November, International Applied Mechanics, Springer New York ISSN1063-7095 (Print) 1573-8582 (Online) Zoran Drašković (2002) Numerical Comparison of The Scalar, Pseudoinvariant And Invariant Approach In The Derivation Of Finite Element Equations Of Motion In Curvilinear Coordinates. FACTA UNIVERSITATIS, Series: Mechanics, Automatic Control and Robotics, Vol.3, No 12, pp. 351 - 357 Gómez Jáuregui, Valentín (2004). Tensegrity Structures and their Application to Architecture, Master's thesis, Belfast, Northern Ireland: Queen's University, School of Architecture in Appendix E SOCIEDAD ESPAŃOLA DE MÉTODOS NUMÉRICOS EN INGENIERÍA, Boletín de Sumarios, SEPTIEMBRE (2004), Nş 43 Icardi U and Atzori A (2004) Simple, efficient mixed solid element for accurate analysis of local effects in laminated and sandwich composites, Advances in Engineering Software 35, pp 843-859 Drašković Zoran (2004) INVARIANCE IN MECHANICS − A CHALLENGE FOR ALL TIMES?FACTA UNIVERSITATIS. Series: Mechanics, Automatic Control and Robotics. 4(16):173 - 182 Jim Wood D5603 - Procedural Benchmarks for Common Fabrication Details in Plate/Shell Structures (Finite element HC8/9) published by NAFEMS-FENet. Icardi Ugo (2006) Layerwise mixed element with sublaminates approximation and 3D zig-zag field, for analysis of local effects in laminated and sandwich composites. International Journal for Numerical Methods in Engineering. on line first Mayhem Sparkles Elmo (2006) Intro Stress Recovery Chapter http://www.mcc.monash.edu.au/twiki/pub/Geodynamics/WendySharplesPhDResearch_SPR/sprintro.pdf Bishnu Prasad Lamichhane. Higher Order Mortar Finite Elements with Dual Lagrange Multiplier Spaces and Applications. Doctoral thesis. 2Institute of Applied Analysis and Numerical Simulations (IANS), UniversitÄat Stuttgart (2006) Chavan KS, Lamichhane BP, Wohlmuth BI, Locking-free finite element methods for linear and nonlinear elasticity in 2D and 3D. Computer Methods in Applied Mechanics and Engineering, 196 (41), p.4075-4086, Sep 2007 G. R. Liu, T. Nguyen-Thoi and K.Y.Lam. A novel FEM by scaling the gradient of strains with factor α ( α FEM), Computational Mechanics, online first, DOI:10.1007/s00466-008-0311-1 (2008) G.R. Liu, T. Nguyen-Thoi, K.Y. Lam. A novel alpha finite element method (aFEM) for exact solution to mechanics problems using triangular and tetrahedral elements, Comput. Methods Appl. Mech. Engrg. 19(7): 3883-3897 (2008) G. R. Liu, H. Nguyen-Xuan, X. Xu. A novel Galerkin-like weakform and a superconvergent alpha finite element method (SαFEM) for mechanics problems using triangular meshes. Journal of Computational Physics, Volume 228 , Issue 11, Pages 4055-4087 (2009) Thanh Ngoc Tran, G. R. Liu, H. Nguyen-Xuan, T. Nguyen-Thoi. An edge-based smoothed finite element method for primal-dual shakedown analysis of structures. International Journal for Numerical Methods in Engineering. Early View (2009) Thanh Ngoc Tran, G. R. Liu, H. Nguyen-Xuan, T. Nguyen-Thoi (2010) An edge-based smoothed finite element method for primal- dual shakedown analysis of structures. International Journal for Numerical Methods in Engineering, 82(7):917-938, DOI: 10.1002/nme.2804

Member of PhD defense board

Procena integriteta kao deo procedure projektovanja zavarenih tankozidnih konstrukcija, Mentor Prof. dr Aleksandar Sedmak, Kandidat mr Emhamed Oman Emhamed Argob, Mašinski fakultet Beograd (2005) Stabilnost i optimalni oblik štapa na elastičnoj podlozi, Doktorska disertacija, Mentor: Prof. dr Teodor Atanacković Kandidat: mr Branislava Novaković, Tehnički fakultet, Univerzitet u Novom Sadu, (2006).

Mentor in MSc thesis

O optimalnom obliku rotirajućih stubova. kandidat: David Braun. Mentor: Prof. dr Teodor Atanacković Tehnički fakultet, Univerzitet u Novom Sadu, (2003) Hibridni super element u ravnom problemu teorije elastičnosti. Kandidat Bogdanović S. Bogdan, Matematički fakultet u Beogradu (2005) O nekim aspektima primene nove primalno - mešovite metode konačnih elemenata u problemima provođenja toplote. Kandidat Ana Žiberna, Matematički fakultet u Beogradu (2006) Verifikacija primalno-mešovite metode konačnih elemenata u problemima provođenja toplote u mehanici čvrstog tela. Kandidat Bojan Međo, Matematički fakultet u Beogradu (2006)

Research History

Research, Development and Implementation of the original Mixed Finite Element Approaches in Semi-Coupled Steady State Heat and Inelastic Mixed Finite Element Analysis The use of the original three-dimensional primal-mixed approaches in more reliable calculation of the thermomechanical response of the laminated microelectronic packaging - the necessary first step in the bridging of the micro and macro analyses Research, Development and Implementation of the original Transient heat finite element solver, based on the mixed finite element approach and its semi-coupling with mixed finite element approach in elasticity Research and development of new reliable scheme for multiscale analysis of solid bodies, where primal-mixed finite element scheme is used in continuum domain and molecular dynamics and embedded-atom interatomic potential is used on atomic scale. Bridging is currently performed on scale of 1E-7m.

Invited Academic Visits

Ecole Polytechnique, Department of Mechanics, Professor Joseph Zarka (2005) Florida International University, Department of Mechanical and Materials Engineering, Professor George S Dulikravich (2005) Universitat Politčcnica de Catalunya, The International Center for Numerical Methods in Engineering (CIMNE), Professor Eugenio Onate (2007) National Institute of Standards and Technology, Gaithersburg, MD, USA (2007) SFTC Rutherford Appleton Laboratory, Harwell Science and Innovation Campus, Academician Professor Iain Duff (2007) CERFACS - The European Centre for Research and Advanced Training in Scientific Computation, Toulouse, France (2008) Aristotle University Thessaloniki, Department of Mechanics (2009) National Institute for Fusion Science, Department of Helical Plasma Research, Japan (2011) University of Stuttgart, Institute for Materials Testing, Materials Science and Strength of Materials (IMWF), Germany (2012)

Developed FEA Software modulus (Original approaches)

POSTFEA - Finite Element Graphical Postprocessor (1993) FEGSS - Global Coordinate Independent Stress Recovery Technique from Stress field calculated in raw finite element displacement method (1993) FEDSS - Global Coordinate Independent Stress Recovery Technique from Displacement field calculated in raw finite element displacement method (1995) FEPRIM - Coordinate Independent 2D Displacement Based Finite Element Method (1995). FEMIX2D - Plain stress/strain reliable coordinate independent primal-mixed FE Scheme, displacement and stresses solution variable, 2 order of magnitude efficient than raw finite element displacement approach with same integration scheme). Reliability consistency, elipticity, inf-sup test (1997) FEMIX3D - Fully 3D coordinate independent reliable primal-Mixed FE approach In elastostatics, displacement and stresses solution variable, reliable hexahedral finite element HC8/27, robust to drastic changes in shape robust in near incompressibility, arbitrary b.c. per stress/displacements, initial displacement/stress, residual stress, robust near singularities, on material interfaces (2001) FEMIX3DT (HC) -FEMIX3D + initial thermal strain field (2002) FEMIX-PLAST (HC)- FEMIX3D + Zarka’s approach in inelasticity (2003) FEMIX-SH (HC) - Fully 3D coordinate independent reliable primal-mixed FE approach In Steady State Heat Analysis, temperature and heat flux solution variables chosen from continuous approximation spaces. Initial temperature / heat flux (2004) FEMIX-MFET (HC) - Semicoupling of FEMIX-SH and FEMIX3DT for thermo‑mechanical analysis. Hexahedral FE HC8/27, no consistency error (2004) FEMIX-TH (HC) - Fully 3D coordinate independent reliable primal-mixed FE approach in Transient heat analysis, hexahedral FE HC8/27 (2004) FEMIXTM - Semicoupling of FEMIX-TH and FEMIX3DT for thermo‑mechanical analysis. Hexahedral FE HC8/27, no consistency error (2004) FEMIXTM+MD - One to one bridging of FEMIXTM with molecular dynamics approach developed by Mastilovic S. (2005) FEMIXTM+HSL Time efficient approach in thermo-mechanical analysis of solid bodies over the geometrical scales and material properties, based on FEMIXTM where Rutherford Appleton Laboratory HSL routines developed by Prof. Iain Duff are used for the solution of the resulting large system of linear equations, As being time efficient, present approach enables full scale analysis of complex engineering structures, such as wind turbines, nuclear reactor core, or coated components. It is robust in near incompressible case, and can reliably analyze multimaterial engineering components, as sandwich composite panels with foam in its core. It is in variance with abundantly used primal finite element approach which suffers of several types of locking effects in aforementioned examples, and requires dimensional reduction if thick or thin solid bodies are analyzed. The semi—coupling between with other field problems, such as electromagnetical or moisture diffusion, is enabled also (2005) Apr 10 , 2019. Zurich

About

ACADEMIC AND INDUSTRY PROFESSIONAL IN CAE AND MATERIALS Professional orientation: • Numerical modeling of the physical laws and implementation into efficient code • Thermo-mechanical Finite Element (FEM) development • Thermo-mechanical Finite Element (FEM) Analysis, compliance with standards • Composite material parameters identification, testing, and simulation • Topology design: shape/material, cost/performance analyses of structures • Assessment of carrying capacity and fatigue strength. • Minimization of energy consumption and CO2 emission in buildings and heating devices • Acquisition of new industrial projects and clients • Acquisition of research projects, Management of projects and teams • The organization, facilitating and reporting of events • Partnership with relevant actors Expertise in FEM • Static, dynamic, transient heat transfer, thermo-mechanical, linear, nonlinear, contact, modal, fatigue

Work experience

• Full Professor / Prof.dr / 2007 – Present University UNION - Nikola Tesla, Belgrade, Belgrade, Serbia Accreditation of new curricula for Bachelor, Master and PhD students. Leading, coordination, and management of scientific projects. Lecturing in Mechanics, Finite Element Analysis, Energy Efficiency and Sustainable development. Development of new FEM methods and tools. • Simulation Engineer / 2019 Straintec AG, Zürich, Switzerland Creating FE models such as roller coaster vehicle chassis. Assessment of carrying capacity and fatigue strength. Calculations of machine parts such as axles and shafts according to FKM. Preparing of the auditable documentation. • Calculation Engineer / 2018 SAS Ingenieurbuero AG, Arbon, Thurgau, Switzerland The first validated thermomechanical analysis of wire rope with extruded round polyethylene as a core, under fire hazard. Redesign of coffee heating devices to lower energy consumption. Validation of the performance of railway chassis. Tailoring of the composite materials. • Technical Director / 2010 - 2018 VND inženjering i konsalting doo. Belgrade, Serbia Establishment of the Laboratory for Numerical Simulation and the development of the new measurement instrument for WIFI measurement of acceleration and displacement. FEM/Structural Calculations for various customers in the construction, automotive, and mechanical industries. Design and analysis of railway bogie/gearbox, fire protection doors, rotary kilns, girth gears, soil-pile interaction, etc. Achieving to win the new clients through introducing the new more accurate original technology in soil/pile calculation and bearing capacity of the pile using a new finite element technique, resulting in 18% less steel for pile reinforcement. Achieving to decrease prototype phase to 1 of fire protection door. Preparing the quotas for clients. • Prof. dr / 2012-2013 University of Stuttgart, Institute for Materials Testing, Materials Science and Strength of Material, Stuttgart Area, Germany Introducing a new original conceptual design of the new lightweight original impact protection system, decreasing the price while increasing human safety. Identification of material properties of the particle reinforced composites (polyamide/silica) using FEM/ABAQUS in order to decrease the price while increasing the performance. • Associate Professor / 2000 -2007 Faculty of Mathematics, University of Belgrade, Belgrade, serbia • Main responsibilities: Leader of Seminar of Rheology, Leader of scientific projects, Organisation of scientific events, • Teaching subjects: Computational mechanics, Continuum mechanics, Theory of elasticity, Statics, Theory of oscillation, Mathematics I, Statistic and probability. • Development of a new original finite element method for multiscale multifield thermo- mechanical analysis. Teaching assistant 1990 - 2000

Top

Dubravka Mijuca PhD

CV

About Work experience Education Courses Functions Honors and Awards Professional Society Membership Coordinator of Leader of Other Activities Research Interest Projects: • Projects in Fields of Basic Research • Projects in Energetic Efficiency • International Projects • Projects in Fields of Innovative Research • Industrial projects Reviews / Editorial Jobs Organized events: • Organized workshops • Organized conferences Publications: • Journal Publications and Theses • Cited in • SciTopics Page Elsevier • Books Conferences: • Invited / Plenary Lectures • Invited Lectures at Workshops • Invited Lectures at International Seminars • Fully-Refereed Interntl Conference Proceedings • International Conference Abstract Proceedings • Fully-Refereed National Conference Proceedings • National Conference Abstract Proceedings • Lectures on Domestic Seminars Technical Innovations Studies Reports Research History from 2003. Invited Academic Visits. Developed FEA Software modulus on Original research

Gallery

FEA industry reports.

© 2020

© 2020

Contact

FEMIX HC

Dubravka Mijuca, PhD Comp. Mechanics Zurich, Switzerland t: +41 76 74 915 04 e: dmijuca@swissonline.ch www.dmijuca.in.rs